Unidad 2. Funciones
2.1 Concepto de variable función, dominio, codominio y recorrido de una función

“Una función es una ecuación matemática que relaciona los elementos de un conjunto con un solo elemento de otro conjunto”.

El objetivo principal de leer sobre funciones es ser capaz de resolver las relaciones de las mismas, las funciones formulan las relaciones en forma de ecuaciones y al resolver estas se obtienen las respuestas.

Para comprender con mayor profundidad las funciones, es importante entender lo que es una variable.

Una variable puede ser considerada como un elemento o artículo que puede ser medido en términos cuantitativos o puede entenderse como un elemento que puede ser representado por un número para medir su magnitud.

Su nombre se mantiene así que lo que varía son los valores, es decir, su valor cambia para diferentes valores de entrada.

El dominio de una función es el conjunto de números para los cuales la función está bien definida

,

y el rango es el conjunto de todos los valores que toma la función al variar en su dominio

. 

2.2 Funcion inyectiva, suprayectiva y biyectiva

Función Inyectiva (uno a uno): Una función f es inyectiva si, cuando f(x) = f(y), x = y.

Ejemplo: f(x) = x² del conjunto de los números naturales  a  es una función inyectiva.(Pero f(x) = x² no es inyectiva cuando es desde el conjunto de enteros 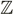 (esto incluye números negativos) porque tienes por ejemplo

• f(2) = 4 y
• f(-2) = 4)

Una función f (de un conjunto A a otro B) es sobreyectiva si para cada y en B, existe por lo menos un x en Aque cumple f(x) = y, en otras palabras f es sobreyectiva si y sólo si f(A) = B.

Así que cada elemento de la imagen corresponde con un elemento del dominio por lo menos.

Ejemplo: la función f(x) = 2x del conjunto de los números naturales  al de los números pares no negativos es sobreyectiva.

Sin embargo, f(x) = 2x del conjunto de los números naturales  a  no es sobreyectiva, porque, por ejemplo, ningún elemento de  va al 3 por esta función.

Una función f (del conjunto A al B) es biyectiva si, para cada y en B, hay exactamente un x en A que cumple que f(x) = y

Alternativamente, f es biyectiva si es a la vez inyectiva y sobreyectiva.

Ejemplo: La función f(x) = x² del conjunto de números reales positivos al mismo conjunto es inyectiva y sobreyectiva. Por lo tanto es biyectiva.

(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo

• f(2)=4 y
• f(-2)=4)

2.3 Función real de variable y su representación gráfica

Cualquier función cuyo rango de conjunto incluya sólo números reales es llamada una función valorada real o simplemente una función real.

Al igual que en cualquier otra función, también a una función real pueden realizársele las operaciones básicas, tales como suma, resta, multiplicación, etc.

Ejemplo, y = 12, en este caso una línea paralela al eje x que pasa por el 12vo punto formará la gráfica.

2. Función Identidad y Gráfico: Una función identidad es una función f: X → Y que tiene la propiedad f(x) = x se mantiene cierta a los elementos de X.

La gráfica de esta función es una línea recta que se traza en un ángulo de cuarenta y cinco grados con el eje x y se extiende en ambos planos negativos y positivos.

Tal función toma un elemento para sí mismo y nunca cambia su dominio. Ejemplo, f (x) = x, en este caso una línea en un ángulo de cuarenta y cinco grados pasa el eje x a travésdel origen y formará la gráfica.

3. Función Módulo y Gráfico: Una función módulo o una función valorada absoluta es una de la siguiente manera, f(x) = x, f(x) = {x >= 0, -x <= 0}

4. Función Recíproca y Grafico: Una función recíproca es una como la que sigue, f(x) = 1/x, donde x <> 0

2.4 Funciones algebraicas: Función polinomial, racional e irracional

Funciones polinomiales

Cualquier función que pueda obtenerse a partir de las funciones constantes y de la función identidad por medio del uso de las operaciones  de suma, diferencia y multiplicación se denomina función polinomial. Esto equivale a decir que “f” , es una función polinomial con la forma:

funciones polinomiales

Donde el entero positivo “n” es el grado de la función polinómica. Las constantes “ai” se denominan coeficientes, siendo “an” el coeficiente dominante y “a0” el término constante.

Funciones racionales

Del mismo modo que un número racional puede escribirse como el cociente de dos enteros, una función f es racional si tiene la forma:

Donde p(x) y q(x) son polinomios. El dominio de estas funciones excluye los ceros del polinomio de q(x). La gráfica de una función racional puede tener asíntotas verticales. Las gráficas de las funciones racionales y de los polinomios tienen varias características en común. Por ejemplo, una función racional solo tiene un número finito de raíces, pues f(x) en la  ecuación.

Funciones irracionales

Del mismo modo que un número irracional no puede escribirse como el cociente de dos enteros, una función f es irracional si tiene la forma

El dominio de estas funciones excluye los valores donde los valores de la raíz son válidos, dependiendo del valor de “n”. Si “n” es par, el radical está definido para g(x)≥ 0; así que a los efectos de calcular el dominio de f(x) que contiene un radical, habrá que imponer la condición anterior al conjunto de la expresión f(x).

2.5 Funciones trascendentes: Funciones trigonométricas y funciones exponenciales

Funciones Trascendentes:

Todas las funciones que se se consideren como no algebraicas son denominadastrascendentes. Mientras tanto las funciones exponenciales, trigonométricas, logarítmicas e hiperbólicas, así como sus inversas, son funciones trascendentes.

Funciones trigonométricas

Una función trigonométrica es importante por el hecho de tener un patrón y ser repetitiva, esto le da la capacidad al que la utiliza de poder interpretar ciertos actos físicos que requieren de cierta repetitividad para funcionar.

Las funciones trigonométricas mas utilizadas son: seno, coseno, tangente, cotangente, secante, cosecante.

Graficas de la función seno, coseno y tangente

Función cosecante

f(x) = cosec x

Grafica de Función cosecante

Función secante

f(x) = sec x

Grafica de función secante

Función cotangente

f(x) = cotg x

Grafica de función cotangente

Funciones exponenciales

f(x)= a^x

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.

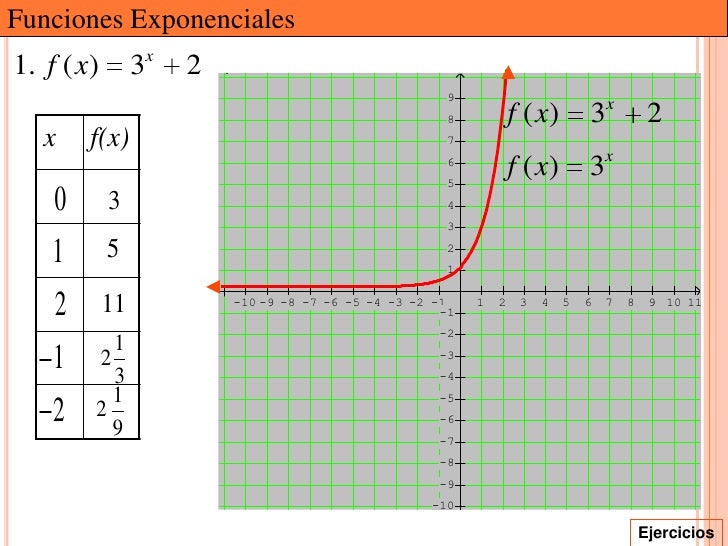
2.6 Función definida por mas de una regla de correspondencia, función valor absoluto

Función a trozos es un nombre más general para una función que puede ser definida con la ayuda de múltiples funciones de correspondencia.

Una función f: X → Y es llamadauna función a trozos si puede ser definida con la ayuda de varias funciones lineales.

Podemos decir que tal función está definida en una serie de intervalos múltiples.

La notación general para definir una función a trozos es la siguiente,

Función valor absoluto

La función de valor absoluto es generalmente una función par, ya que cualquier número y su equivalente negativo tienen los mismos valores absolutos. Tal función es estrictamente decreciente en el intervalo (- ∞, 0] y estrictamente creciente en el intervalo [0, ∞). El ejemplo ilustrado arriba es también una función de valor absoluto.

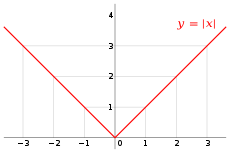
2.7 Operaciones con funciones: Condición, multiplicación, composición
Suma denotada por f + g es la funcion definida (f+g) (x) = f(x) + g(x)

Su diferencia denotada por f-g es la funcion definida (f-g)= f(x) - g(x)

Su producto denotado (f)(g) es la funcion definida por [f(x)][g(x)]

Su cociente denotado por f/g es la funcion definida de f/g = f(x)/g(x)

Ejercicios: Resuelve las siguientes operaciones

f(x) 3x - 1     g(x) 4 - x

1.-F(x) + g(x)

2.- f(x) - g(x)

3.- f(x) . g(x)

4.- f(x)/g(x)

f(x) 4x+5     g(x) x

1.-F(x) + g(x)

2.- f(x) - g(x)

3.- f(x) . g(x)

4.- f(x)/g(x)

f(x) 1/x       g(x)  2x

1.-F(x) + g(x)

2.- f(x) - g(x)

3.- f(x) . g(x)

4.- f(x)/g(x)

2.8 Función inversa, logarítmica y trigonométricos inversas

Se llama función inversa o reciproca de f a otra función f−1 que cumple que:

Si f(a) = b, entonces f−1(b) = a.

Básicamente se esta dando a entender que al invertir las variables en la función normal y en la función inversa estas deben dar como resultado la variable de la función anterior.

Veamos un ejemplo a partir de la función f(x) = x + 4

Segun podemos observar en la figura, el dominio de  f−1 es el recorrido de f.

Por otra parte el recorrido de f−1 es el dominio de f (Esto ejemplifica ese concepto extraño que tratamos de dar al principio).

Basándonos en el mismo principio se establece que si queremos halla el recorrido de una función tenemos que hallar el dominio de su función inversa.

Calcular la función inversa de:

1. 

2. 

3. 

Función logarítmica:

Una función logarítmica corresponde a aquella que se expresa de la forma: f (x) == logax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.

La función logarítmica es considerada como la inversa de la función exponencial, debido a  que:

loga x = b Û ab = x.

unciones trigonométricas inversas:

Las funciones trigonométricas inversas son las funciones inversas de las razones trigonométricas (seno, coseno y tangente).

Las razones trigonométricas no corresponden a las funciones biyectivas (1-a-1), por lo que no son invertibles. Para que lo sean, es necesario restringir su dominio y así poder hallar la función inversa.

Arcoseno

El arcoseno es la función inversa del seno. Es decir:

Al ser el arcoseno y el seno funciones inversas, su composición es la identidad, es decir:

Su abreviatura es arcsen o sen-1.

• Dominio (x): 
• Codominio (α): Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función seno no es inyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [-π/2,π/2] para que la función seno sea biyectiva.
• La función es continua y creciente en todo el dominio.
• Derivada de la función arcoseno: 

Arcocoseno

El arcocoseno es la función inversa del coseno. Es decir:

Al ser el arcocoseno y el coseno funciones inversas, su composición es la identidad, es decir:

Su abreviatura es arccos o cos-1.

• Dominio (x): 
• Codominio (α): Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función cosenono es inyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [0,π] para que la función coseno sea biyectiva.
• La función es continua y decreciente en todo el dominio.
• Derivada de la función arcocoseno: 

Arcotangente

La arcotangente es la función inversa de la tangente. Es decir:

Al ser la arcotangente y la tangente funciones inversas, su composición es la identidad, es decir:

Su abreviatura es arctan o tan-1.

• Dominio (x): 
• Codominio (α): Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función tangenteno es inyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [-π/2,π/2] para que la función tangente sea biyectiva.
• La función es continua y creciente en todo el dominio.
• Derivada de la función arcotangente: 

Ejercicio: Explicar el por que de estos resultados.

2.9 Funciones con dominio en los números naturales y recorrido en los números reales: las sucesiones infinitas

Una secuencia infinita puede ser definida como un conjunto ordenado o una lista de elementos distintos que pueden ser formados como pares teniendo correspondencia uno a uno respecto al conjunto entero positivo. Los elementos son por lo general números. Un conjunto de números naturales es un buen ejemplo de sucesión infinita, N = {0, 1, 2, 3, 4…}.

En términos de la notación matemática, una secuencia puede ser definida como una función sobre F U {0} ya que la función g (x) tiene una asociación uno a uno de F en F U {0}.

La secuencia infinita forma una parte importante de los estudios de la ingeniería y la física moderna. Una secuencia infinita puede estar creciendo, decreciendo, o ser de origen monótona. Una sucesión creciente es aquella donde todos los elementos subsecuentes de la secuencia son mayores que el elemento que estaba ocurriendo antes que ellos en la secuencia, esto es an+1 > an para todos los valores de n.

Una secuencia decreciente infinita es opuesta a la sucesión creciente infinita lo que significa que en el caso de una secuencia decreciente infinita el elemento subsecuente de la secuencia es más pequeño que el elemento que estaba ocurriendo antes que este en la secuencia, esto es un an+1 < an para todos los valores de n.

Mientras que una secuencia infinita monótona puede ser una que esté creciendo o decreciendo.

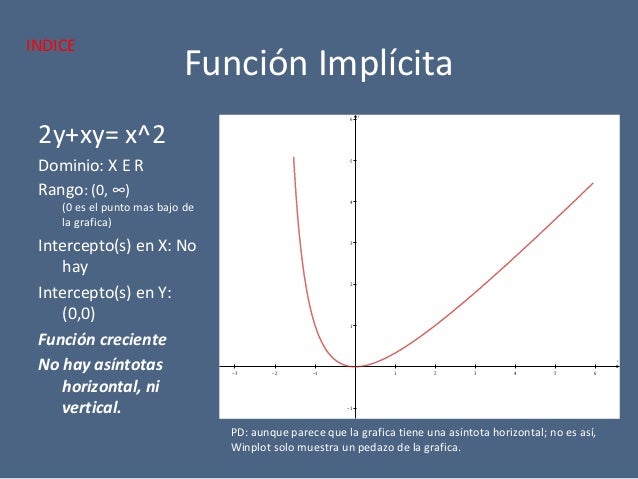
2.10 Función implícita

Una función implícita también se conoce como un conjunto de nivel de cualquier función en términos de dos variables. Fuera de esas dos variables, una de ellas se puede determinar con la ayuda de otra variable. Pero no existe ninguna fórmula específica para determinar una variable en términos de otra variable.

Las funciones implícitas y las funciones explícitas están relacionadas entre sí con la ayuda del teorema de la función implícita. Según este teorema, si la función implícita satisface algunas de las condiciones, aunque levemente, sobre sus derivadas parciales entonces es posible resolver esta función para determinar el valor de y, al menos para un rango pequeño.

Si nos fijamos en la gráfica de una función implícita, nos encontraríamos con que su gráfica se superpone con la gráfica de la función f(x) = y, localmente.

Para tener una mejor comprensión, veamos el ejemplo dado a continuación,

Aquí x es una función implícita en términos de y, también y es una función implícita en términos de x. Para resolver la ecuación para la variable y, la ecuación se convertiría,

En la ecuación anterior, y es la función explícita de x. En el penúltimo ejemplo era fácil resolver la ecuación para y en términos de x, pero hay ocasiones en que la función dada es mucho más compleja y no se puede resolver fácilmente.