lunes, 30 de noviembre de 2015

Unidad 3 Limites y continuidad

3.1 Limite de una sucesión 
El límite de una sucesión es el número al cual se van aproximando los términos de una sucesión.
Cálculo del término general de una sucesión
a1= 1
a2= 0.5
a1000= 0.001
a1000 000 = 0.000001
El límite es 0.
Cálculo del término general de una sucesión
a1= 0.5
a2= 0.6666....
a1000= 0.999000999001
a1000 000 = 0.999999000001
El límite es 1.
sucesión
a1= 5
a2= 7
a1000= 2 003
a1000 000 = 2 000 003
Ningún número sería el límite de esta sucesión, el límite es ∞.
Ejercicios:

3.2 Limite de una función de variable real
Se le llama función real de variable real a toda la función definida de un subconjunto D de los números reales, en el conjunto R de los números reales, tal que a cada elemento x de D le corresponde uno y sólo un elemento y de R:
f:D————->R
x————->x2.
Para que una función quede correctamente definida es necesario determinar:
  1. El conjunto inicial o dominio de la función.
  2. El conjunto final o imagen de la función.
  3. La regla por la cual se asigna a cada elemento del conjunto origen un solo elemento del conjunto imagen.
Así, por ejemplo, la función definida por:
f:R ——–>R
x———>x2.
asigna a cada número real su cuadrado.
Tiene por conjunto origen o campo de existencia todos los números reales, pues dado cualquier número real x, siempre es posible calcular su cuadrado, siendo el resultado otro número real.
Tiene por conjunto imagen todos los números reales positivos, puesto que el cuadrado de un número siempre es positivo:
lim(f)=R+.
La regla de asignación es: “Dado cualquier número real x, calcular su cuadrado para obtener la imagen”.
Algunos ejemplos explicados podrán consultarlos en este link:
https://www.youtube.com/watch?v=tJMM6lmXNkM
3.3 Calculo de Limites
Si f(x) es una función usual (polinómicas, racionales, radicales, exponenciales, logarítmicas, etc.) y está definida en el punto a, entonces se suele cumplir que:
límite
Es decir: Para calcular el límite se sustituye en la función el valor al que tienden las x.
Cálculo del límite en un punto
Cálculo del límite en un punto
Cálculo del límite en un punto
No podemos calcular límite porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.

3.4 Propiedades de los limites
En la definición de limites de una función  de la sección 3.1 se determinaba la existencia  de un límite en base a una gráfica o tabla de valores númericos, por lo que esto no es práctico y es aconsejable evaluar los limites de manera análitica.Para ello es importante considerar y utiolizar las propiedades de los límites:

Así mismo consideraremos los limites de las funciones trigonométricas, dadas como continuación de la tabla 
3.5 Limites laterales
Consideremos la siguiente representación gráfica de una función 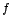$f$, en la que existe una discontinuidad cuando $x=a$:
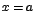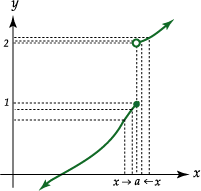notemos que cuando $x$ tiende hacia "a" por la derecha de "a" la función tiende a 2, pero cuando $x$ tiende hacia "a" por la izquierda de "a", la función tiende hacia 1.
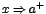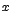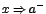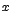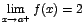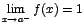Escribimos $x\Rightarrow a^{+}$ para indicar que $x$ tiende hacia "a" por la derecha, es decir, tomando valores mayores que "a". Similarmente $x\Rightarrow a^{-}$ indica que $x$ tiende hacia "a" por la izquierda, o sea, tomando valores menores que "a". Utilizando ahora la notación de límites, escribimos $\displaystyle {\lim_{x \rightarrow{a^{+}}}{f(x)}=2}$ y $\displaystyle {\lim_{x \rightarrow{a^{-}}}{f(x)}=1}$. Estos límites reciben
el nombre de límites laterales; el límite por la derecha es 2 y el límite por la izquierda es 1. 
Ejemplo:
Determinaremos los límites en los puntos de discontinuidad de la función $h$ cuya representación gráfica es la siguiente:
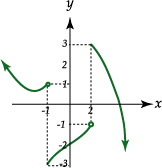Se tiene que:
$\displaystyle {\lim_{x \rightarrow{2^{+}}}{h(x)}=3}$ y $\displaystyle {\lim_{x \rightarrow{2^{-}}}{h(x)}=-1}$
$\displaystyle {\lim_{x \rightarrow{-1^{+}}}{h(x)}=-3}$ y $\displaystyle {\lim_{x \rightarrow{-1^{-}}}{h(x)}=1}$
3.6 Limites infinitos y limites al infinito
Decimos que lim f(x)=\infty si para los valores de x proximos a a,     x→ a    los valores de f(x) pueden hacerse tan grandes como queramos.
Con rigor, decimos que lim f(x)=\infty si fijado a un valor k positivo y tan grande como se quisiera, existe un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entoces f(x)>k.
Análogamente,    lim f(x) = – \infty
x→a 
si para los valores de x cercanos a a, los valores de f(x) se pueden hacer tan pequeños como queramos.
Diremos que lim f(x) = – \infty
x→a 
si fijado un valor de k positivo y tan grande como se quisiera, podemos encontrar un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entonces  f(x) < -k
•Ejemplo:
la función f(x)= 1/|x|
En el punto x=0 se tiene:
lim 1/|x| = – \infty
x→ 0-
→ lim    1/|x| = \infty                                               x→0 
lim 1/|x| = \infty
x→a’
||LIMITES AL INFINITO||
cuando el dominio de y= f(x) se extiende indefinidamente hacia la derecha o hacia la izquierda de la recta real tienen sentido las expresiones:
• lim f(x) = L si “haciendo x arbitrariamente grande”, los valores de f(x) se acercan a L.
x→ \infty
•lim f(x) = L si “haciendo x arbitrariamente pequeña, los valores de f(x) se acercan a L.         x→\infty

3.7 Asintotas
Si un punto (x,y) se desplaza continuamente por una función y=f(x) de tal forma que, por lo menos, una de sus coordenadas tienda al infinito, mientras que la distancia entre ese punto y una recta determinada tiende a cero, esta recta recibe el nombre de asíntota de la función.
Las asíntotas se clasifican en:

  1. Asíntotas verticales (paralelas al eje OY)
    Si existe un número “a” tal, que :
    La recta “x = a” es la asíntota vertical.
    Ejemplo:
     es la asíntota vertical.
  2. Asíntotas horizontales (paralelas al eje OX)
    Si existe el límite: :
    La recta “y = b” es la asíntota horizontal.
    Ejemplo:
     es la asíntota horizontal.
  3. Asíntotas oblicuas (inclinadas)
    Si existen los límites: :
    La recta “y = mx+n” es la asíntota oblicua.
    Ejemplo:
     es la asíntota oblicua.

3.8 Funciones continuas y discontinuas en un punto y en un intervalo
Una función continua es aquella que responde a las variación es de cada minuto en la entrada de la función por lo que muestra variación en la salida de la función.
Una definición formal de una función continua es “Una función f: X → Y se dice que es continua, si la imagen inversa de todos los conjuntos abiertos en el rango de la función son abiertos en el dominio de la función”.
Para que una función continua sea continua en un punto P específico, debe cumplir tres condiciones:
1. El punto s debe estar en el dominio de la función, en otras palabras la función f(s) debe tener un valor definido.
2. Para un punto a en el dominio de la función,
 debe mantenerse verdadero en el dominio de la función dada 
3. La ecuación debe mantenerse verdadera para la función ylos puntos dados.
Observe un ejemplo a continuación
g(x) = x2 – 9/x – 3
La función dada no es de naturaleza continua, porque el punto 3 no se encuentra en el dominio de la función dada.
Si la inversa de la función, en conjunto con la función misma, es continua, entonces la función es llamada función bicontinua.
Sin embargo, una función también puede sercontinua en un rango de intervalo, lo que significa que la función produce un valor definido para todos los puntos en el intervalo dado.
Se hace difícil encontrar tales puntos donde la función no produce ningún valor, o podemos decir cuando es discontinua en tal escenario.
Una simple fórmula para el cálculo de la continuidad es encontrar los valores en los cuales la función no es continua.
El teorema del valor intermedio establece que para una función f: X → Y que es continua en un intervalo [a, b], entonces la función es verdadera para a y b, y para todos los demás puntos entre a y b.
Si a y b tienen signos opuestos entonces hay algún punto entre a y b tal que el valor de la función en ese punto es cero. Observe el ejemplo que se muestra a continuación: g(y) = y +
Dado que se obtiene una cantidad compleja al buscar la raíz cuadrada de un número negativo, se puede concluir que la función dada tiene un valor definido para (1 – y2) cuando equivale igual o mayor que cero, lo que da x <= 1 sea definida para la función y no para un valor menor del que está definido.
Una función que no es continua es llamada función discontinua.
Una función puede ser discontinua en un punto o para un intervalo completo.
Una función que es discontinua en un punto debe cumplir dos requisitos:
• Tanto del lado izquierdo así como del derecho debe existir un límite para la función en el punto dado.
• Ambos límites deben ser finitos naturales.
Si la discontinuidad puede ser eliminada entonces es de primer orden, mientras que si no puede ser eliminada se conoce como discontinuidad de segundo orden.
Al observar la gráfica de una función discontinua esta puede ser claramente separada del resto ya que su gráfica se suele dividir en dos partes más.
Similar a una función continua, la discontinuidad puede también durar más de un intervalo finito.

3.9 Tipos de discontinuidad

Discontinuidad evitable

Si una función tiene límite en un punto, pero la función en ese punto tiene un valor distinto:
asodiaosdio1
o no existe:
qwoiuwqoiqwiq
se dice que la discontinuidad es evitable, asignando a la función, en ese punto, el valor del límite:
0p021ñpñsas

Discontinuidad esencial o no evitable

Se dice que una función presenta una discontinuidad esencial cuando se produce algunas de las siguientes situaciones:
  1. Existen los límites laterales pero no coinciden.
  2. Alguno de los límites laterales o ambos son infinitos.
  3. No existe alguno de los límites laterales o ambos.

Discontinuidad de primera especie

En este tipo de discontinuidad existen tres tipos:
– DE SALTO FINITO
Existen el límite por la derecha y por la izquierda del punto, su valor es finito, pero no son iguales:
A este tipo de discontinuidad de primera especie se le llama salto finito, y el salto viene dado por:De salto infinitoSi uno de los límites laterales es infinito y el otro finito, tanto si el límite por la izquierda es finito y el de la derecha infinito:
como en el caso de que el límite por la izquierda sea infinito y por la derecha finito:
masdnasdkj
Se dice que la discontinuidad es de salto infinito.
DISCONTINUIDAD ASINTÓTICA
Si los dos límites laterales de la función en el punto x= a son infinitos:
aspodadipq
A este tipo de discontinuidad de primera especie se le llama discontinuidad asintótica, siendo x= a la asíntota.

Discontinuidad de segunda especie


Si la función no existe en uno de los lados del punto, o no existen alguno, o ambos, de los límites laterales de la función en ese punto, se dice que la función presenta una discontinuidad de segunda especie en ese punto.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)